Artigo Completo

Método de Polya e problemas verbais: estratégias de linearização sintático-semânticas

Inês Trindade Monteiro

Escola Superior de Educação do Politécnico do Porto

Daniela Filipa Martinho Mascarenhas

Escola Superior de Educação do Politécnico do Porto/ CeiED/ inED

Celda Maria Gonçalves Morgado

Escola Superior de Educação do Politécnico do Porto/ CLUP/ inED

RESUMO

Neste artigo, apresentar-se-ão resultados parciais de uma investigação que recaiu sobre a compreensão de problemas verbais e a aplicação do método de Polya, no 4.º ano/1.ºCEB.A investigação desenvolveu-se segundo duas questões-problema: O domínio das competências de compreensão na Leitura influencia a resolução de problemas?; Que contributo poderá ter, para os alunos, o conhecimento do método de Polya e de diferentes estratégias na resolução de problemas verbais de dois ou mais passos?. Seguiu a metodologia de investigação-ação, com abordagem mista. Aplicou-se um teste com duas versões: v.A, três problemas verbais extraídos das Provas de Aferição (2015); v.B, os mesmos problemas adaptados semântica e sintaticamente. Fases: aplicação do (pré-)teste; intervenção, incidindo na articulação das fases do método de Polya com as componentes da compreensão na leitura e no ensino de estratégias de compreensão na resolução de problemas verbais; reaplicação do (pós-)teste. Apresentaremos apenas os dados relativos aos problemas com alterações semânticas. Os resultados do pós-teste foram superiores aos do pré-teste: no problema1, na v.B a média subiu 0.45 pontos; no problema3, na v.A 0.94 e na v.B 1.29. Demonstrar-se-á a importância de uma aprendizagem articulada, visto que a língua materna é o veículo de comunicação no ensino da Matemática.

Palavras-chave: domínio metalinguístico; resolução de problemas verbais; método de Polya; estratégias de compreensão na leitura

ABSTRACT

In this paper, we will present partial results of an investigation that fell on the understanding of verbal problems and the application of the Polya method, in 4th grade Primary School. The research was developed according two problemquestions: Does the domain of comprehension skills in Reading influence problem solving?; What contribution can the students have to the knowledge of the Polya method and of different strategies in solving verbal problems of two or more steps?. It followed the research-action methodology, with a mixed approach. A test was applied with two versions: v.A, three verbal problems extracted from the Verification Tests (2015); v.B, the same problems adapted semantically and syntactically. Phases: application of the pre-test; intervention, focusing on the articulation of the phases of the Polya method with the components of comprehension in reading and teaching comprehension strategies in the resolution of verbal problems; reapplication of the post-test. We will only present data on problems with semantic changes. The results of the post-test were higher than those of the pre-test: in problem 1, in v.B the mean rose by 0.45 points; in Problem 3, in v. A 0.94 and v.B 1.29. The importance of articulated learning will be demonstrated, since the mother tongue is the vehicle of communication in the teaching of Mathematics.

Keywords: metalinguistic domain; verbal problem solving; polya method; comprehension strategies in reading

INTRODUÇÃO

O olhar observador sobre a realidade vivenciada no ensino da Matemática desperta uma reflexão sobre os fracos resultados académicos, nesta área de saber, sobretudo, na resolução de problemas com enunciados verbais.

Deste modo, e dado que a resolução de problemas possui um papel fundamental na formação do aluno, visto ser um instrumento primordial da sua aprendizagem, uma vez que potencializa o desenvolvimento de capacidades necessárias à tomada de decisões, e, consequentemente, melhor qualidade de vida (UNESCO, 1990), é necessário uma reflexão sobre o insucesso dos alunos nesta área de saber. Assim, a partir da nossa observação verifica-se que os alunos possuem sucesso na resolução de problemas de aplicação de conteúdo, compreendendo o que é solicitado, e a sua dificuldade centra-se na aplicação dos conteúdos matemáticos. Quando são apresentadas tarefas que envolvam a resolução de problemas, estes demonstram dificuldades na compreensão do enunciado verbal, na identificação dos dados e, paralelamente, na identificação de estratégias adequadas para a resolução do problema, não conseguindo aplicar os conteúdos programáticos apreendidos. Dellarosa, Kintsch, Reusser e Weimer (1988, citado por Valentin & Sam, 2004) corroboram esta reflexão quando asseveram que o insucesso dos estudantes nos problemas matemáticos com enunciados verbais resulta da falta de conhecimento linguístico. Também o projeto desenvolvido, a nível nacional, sobre Leitura, compreensão e usabilidade dos problemas de matemática com textos bimodais mistos (Baptista, no prelo) apresenta os mesmos resultados: muitos dos erros dos alunos, na resolução de problemas verbais, advém das baixas competências linguísticas e textuais (da estrutura específica deste tipo de texto) e, ainda, do facto de muitos destes problemas serem apresentados como bimodais e as ilustrações típicas dos materiais didáticos e das provas de avaliação não facilitarem a compreensão dos conteúdos e dos problemas matemáticos. De referir ainda que o estudo exploratório desenvolvido por Monteiro (2018) apresenta resultados semelhantes no que se refere às dificuldades de compreensão dos enunciados verbais e às estratégias de compreensão na Leitura e de resolução dos problemas. 

Posto isto, e tendo como ponto de partida que as grandes diferenças observadas entre as duas tipologias de problemas, problemas simbólicos nãoverbais e problemas verbais, são a linguagem em que o enunciado se encontra apresentado e, consequentemente, a forma ou configuração geral daí decorrente, torna-se importante averiguar se a compreensão na leitura, a identificação e seleção dos dados e a interpretação dos mesmos estarão interligados e cooperam para os baixos resultados na resolução de problemas verbais e não-verbais.

Neste seguimento, delinearam-se cinco objetivos específicos par realizar o presente estudo: i) contribuir para a identificação das dificuldades dos alunos do 4.º ano de escolaridade na resolução de problemas verbais de dois ou mais passos; ii) compreender a influência das estratégias incluídas nas várias fases do método de Polya por componente de leitura dos enunciados de problemas verbais; iii) perceber se as estruturas semântica e sintática do enunciado do problema influenciam a resolução dos alunos; iv) analisar o impacto que o conhecimento e a aplicação do método de Polya podem ter no desempenho dos alunos; v) contribuir para formação científica e científico-pedagógica do professor de 1.º Ciclo do Ensino Básico (CEB).

Por sua vez, de modo a definir o design do estudo e atingir aqueles objetivos, formularam-se duas questões de investigação:

-Questão 1: O domínio das competências de compreensão na leitura influencia a resolução de problemas matemáticos?

-Questão 2: Que contributo poderá ter, para os alunos, o conhecimento do método de Polya e de diferentes estratégias na resolução de problemas verbais de dois ou mais passos?

Assim, na primeira parte deste artigo, far-se-á uma breve revisão da literatura sobre a resolução de problemas, a essencialidade do Português e da Matemática e da sua necessária inter-relação e as dificuldades na resolução de problemas. Em seguida, analisar-se-á todo o desenvolvimento do estudo comparativo entre os dados recolhidos nos testes de avaliação de conhecimentos (pré-teste e pósteste), com o intuito de procurar pontos em comum entre as variáveis em estudo, de forma a tentar dar resposta aos objetivos e às questões-problema traçadas.

1.ENQUADRAMENTO TEÓRICO

1.1. A ESSENCIALIDADE DO PORTUGUÊS E DA MATEMÁTICA

Nos dias de hoje, a educação, apresenta como objetivo primordial uma formação integral, visando a construção de cidadãos críticos, conscientes e ativos (Mascarenhas, Maia, & Martínez, 2017), tendo como veículos básicos inerentes de uma sociedade a Matemática, bem como a comunicação linguística, uma vez que diariamente o Homem realiza ações que implicam o raciocínio matemático e a comunicação verbal.

Por sua vez, um dos objetivos - qualidade da educação - delineados no Fórum Mundial de Educação em Dakar, elenca o melhoramento de “todos os aspectos da qualidade da educação e assegurar a excelência de todos, de modo que resultados de aprendizagem reconhecidos e mensuráveis sejam alcançados por todos, especialmente em alfabetização, cálculo e habilidades essenciais para a vida” (UNESCO, 2000, p.20). Consequentemente, o Ministério da Educação considerou a Matemática e a Língua Materna, no nosso caso o Português, como uma das bases de formação do indivíduo no ensino obrigatório.

Segundo Machado (1998, citado por Stival & Lisbôa, 2014), entre estas duas áreas curriculares é percetível a existência de uma relação bilateral, revelada

“através de um paralelismo nas funções que desempenham uma complementaridade nas notas que perseguem uma inibição nas questões básicas relativas ao ensino de ambas” (p. 6).

Seguindo esta linha de pensamento, o Perfil dos alunos à saída da escolaridade obrigatória (Martins et al., 2017) define, na área de desenvolvimento e aquisição das competências-chave Linguagens e textos, que as competências adquiridas na mesma “permitem exprimir e representar conhecimento em várias áreas do saber, conduzindo a produtos linguísticos, (…) matemáticos” (p. 13).

Neste pressuposto, o ensino da Matemática está interligado com a compreensão leitora do aluno, sendo necessário que a formação académica englobe a leitura fluente nas diferentes linguagens, nomeadamente na linguagem Matemática, dado que é impossível a comunicação Matemática sem o uso da língua materna (Stival & Lisbôa, 2014).

1.2. A RESOLUÇÃO DE PROBLEMAS

Na área da Matemática, muitos são os autores que possuem uma definição de problema, mas nos dias de hoje, a utilização do termo problema generalizou-se sendo aplicado para se referir a diversas tarefas matemáticas, não se verificando, maioritariamente, a distinção entre problema e exercício. Posto isto, existe um problema quando se torna difícil encontrar a solução, contudo quando uma tarefa, para alguns alunos, se torna “uma situação rotineira, cujo enfoque reside no treino de um algoritmo ou a aplicação de uma técnica julgada importante para a aquisição e o aprofundamento de conhecimentos” (Sá et al., 2006, p. 11), define-se como exercício.

Paralelamente, pode-se categorizar os problemas consoante o seu enunciado, distinguindo-os em problemas simbólicos não-verbais ou em problemas verbais. Desta forma, os problemas simbólicos não-verbais utilizam, maioritariamente, termos matemáticos, sendo indiciada a sua formulação com verbos como: determina; calcula; considera. Nesta tipologia de problemas, não há articulação com o contexto real, tendo como estratégia a aplicação de fórmulas, generalizações ou expressões numéricas (Correia, 2013).

Em relação aos problemas verbais, estes denominam-se verbais por se enunciarem a partir de termos e expressões da língua podendo enquadrar situações relativas à realidade. Os problemas verbais englobam “os problemas de reconhecimento que visam a identificação ou verificação de conceitos, definições ou propriedades” (Correia, 2013, p. 33), e os problemas que são formulados tendo por base a narração de uma história ou de um contexto real, sendo necessário empregar a interpretação e o cálculo para conseguir solucionar a incógnita do problema (idem).

Para que um problema possua valor educativo, é necessário que os alunos não se cinjam à sua solução, mas que mobilizem conteúdos matemáticos na busca e no propósito da sua resposta. Assim, a resolução de problemas torna-se uma atividade estruturada que desenvolve diversas capacidades cognitivas, uma vez que articula “a organização da informação, o conhecimento de estratégias, as diferentes formas de representação, a tradução de linguagens, a aplicação de vários conhecimentos, a tomada de decisões, a interpretação da solução” (Vale & Pimentel, 2004, p.11).

1.3. RESOLUÇÃO DE PROBLEMAS VERBAIS: FASES DO MÉTODO DE POLYA, COMPONENTES DE COMPREENSÃO NA LEITURA E ESTRATÉGIAS DE RESOLUÇÃO

A resolução de problemas é uma tarefa que muitas vezes é de difícil compreensão por parte dos alunos, pois assume-se como uma área de desenvolvimento com grande complexidade para os alunos, devido ao ideal construído pelos mesmos que consiste numa única solução e estratégia de resolução. Por outro lado, visto que os problemas matemáticos verbais usufruem de enunciados que realizam uma simbiose entre a linguagem natural e a linguagem simbólica, na qual o aluno necessita de conhecimentos linguísticos para os interpretar (Österholm, 2006), as dificuldades patentes na compreensão do enunciado patrocinam os baixos resultados nesta área (Vale & Pimentel, 2004). Lopes e Kato (s.d, citado por Pires, 2014, p. 12) defendem esta mesma ideologia, asseverando que “compreender um texto é uma tarefa difícil que envolve interpretação, descodificação, análise, síntese, seleção, antecipação e autocorreção do que foi lido”.

De acordo com Vale e Pimentel (2004), ”não existe um único método para resolver problemas nem para ensinar a resolver problemas” (p.21). Um dos métodos mais conhecidos e com mais impacto e aplicabilidade no ensino da Matemática foi o método apresentado, em 1973, pelo matemático húngaro George Polya. Desta forma, Polya defendeu o recurso a quatro etapas essenciais para a resolução de problemas, que devem ser seguidas pela seguinte ordem, com o intuito de percorrer um caminho até alcançar a solução do problema: compreensão de um problema; estabelecimento de um plano; execução do plano; e verificação (Polya, 1977).

Neste sentido, paralelamente, às estratégias decorrentes da aplicação do método de Polya, a resolução de problemas desenvolve componentes cognitivas implicadas na compreensão da leitura. Segundo Catalá, Catalá, Molina e Monclús (2001, citado por Viana, et al., 2010) estas classificam-se em componente literal, de reorganização, compreensão inferencial e compreensão crítica. Com efeito, irse-á analisar as quatro fases do método de Polya, articulando-as com as componentes cognitivas de compreensão na leitura.

Deste modo, consideramos que na fase compreensão do problema, primeira fase do método, se mobilizam estratégias que levam à compreensão literal, uma vez que, a partir do reconhecimento da informação do enunciado, é possível identificar os dados, as incógnitas e as situações expostas (Polya, 1973, citado por Vale & Pimentel, 2004; Catalá, et al., 2001, citado por Viana et al., 2010). Saliente-se que, quando o estudante lê o enunciado do problema, este realiza uma representação mental do mesmo, na qual inicia o seu processo de solução. No decorrer desta fase, são ativados os conhecimentos prévios indispensáveis para a resolução do mesmo, verificando-se que, para os alunos compreenderem o problema, estes necessitam de associar a representação mental a uma situação modelo já vivenciada pelos mesmos (Österholm, s.d.).

Tabela 1 - Síntese taxonómica da compreensão na leitura (Viana et al., 2010) articulada com as fases do método de Polya e as estratégias desenvolvidas (Fonte: adaptado de Monteiro, 2018)

Fases de Polya	Componentes cognitivas envolvidas na compreensão da leitura	Competências / Objetivos / Metas	Estratégias
1.ª Compreensão do problema	Compreensão literal	-Reconhece as ideias principais do enunciado do problema -Reconhece os dados principais do enunciado; -Reconhece a sequência dos dados do problema/exercício; -Reconhece as relações de causaefeito.	-Sublinha, destaca ou rodeia a informação relevante; -Coloca entre parênteses ou risca a informação irrelevante; -Anota ao lado do problema a informação relevante ao mesmo tempo que lê/ouve ler.
2.ª Estabelecimento de um plano	Reorganização	-Organiza de acordo com as estratégias adequadas a informação do enunciado; -Sintetiza a informação do enunciado; -Organiza a informação segundo uma ordem relevante	-Lista a informação relevante; -Realiza um esquema-síntese; -Realiza um desenho; -Regista os dados por ordem necessária à resolução;
3.ª Execução do plano	Compreensão inferencial	-Deduz a sequência do enunciado; -Deduz uma relação de causa-efeito; -Interpreta a linguagem figurativa.	-Faz tentativas ou conjeturas; -Trabalha do fim para o início; -Faz uma experimentação; -Faz um desenho, diagrama, gráfico ou esquema.
4.ª Verificação	Compreensão crítica	-Formula juízos de valor sobre aceitabilidade (dos dados) -Formula juízos de validade e suficiência.	-Revê as estratégias utilizadas na fase anterior e confirma o resultado, confrontando-o com experiências anteriores e reais.

A segunda fase do método, estabelecimento de um plano, articula-se com a componente de reorganização, em que o aluno, após a sistematização da informação, anteriormente identificada, selecionada e consolidada, procede à reestruturação da mesma, com base nos seus conhecimentos prévios, desenvolvendo mentalmente uma estratégia de resolução, a fim de alcançar a solução. 

A compreensão inferencial é alcançada aquando da execução do plano, terceira fase do método, visto que o aluno, ao executar a sua estratégia, averigua a sua viabilidade, formulando e conjeturando sobre as informações e, caso se verifique necessário, desenvolvendo uma nova estratégia. Por fim, a verificação é a fase de análise da estratégia realizada, quarta e última fase do método de Polya, é o momento da compreensão crítica, comprovando-se o resultado com base na criação de ideologias próprias (Polya, 1973, citado por Vale & Pimentel, 2004; Catalá, et al., 2001, citado por Viana et al., 2010). 

Na Tabela 1, é apresentada a articulação das componentes cognitivas da compreensão na Leitura com as fases do método de Polya e as estratégias desenvolvidas em cada etapa do método de resolução de problemas verbais.

Deste modo, a relação dos problemas verbais de Matemática com a compreensão da informação presente no seu enunciado é um elemento crucial para a compreensão do problema, as estratégias desenvolvidas e, por fim, para uma solução que demonstre a consolidação dos conteúdos matemáticos, sendo notória a necessidade de articulação destas duas áreas curriculares (Choupina, no prelo).

2. O ESTUDO EXPLORATÓRIO

2.1. METODOLOGIA E DESENVOLVIMENTO DA INVESTIGAÇÃO

A investigação no ensino “é uma atividade de natureza cognitiva que consiste num processo sistemático, flexível e objecto de indagação que contribui para explicar e compreender os fenómenos educativos” (Pacheco, 1995, p.9). Consequentemente, a investigação permite que os docentes reflitam e problematizem o ensino e os conhecimentos adquiridos pelos alunos de forma a edificar novos ideais (Máximo-Esteves, 2008).

Neste sentido, o estudo realizou-se seguindo o ciclo de investigação-ação, na qual emprega uma abordagem mista, isto é, utiliza métodos qualitativos e quantitativos de forma a compreender a ação e as ideologias dos investigados, a partir de um espírito “exploratório, expansionista, descritivo e indutivo” (Carmo & Ferreira, 2008, p.195). Por sua vez, esta abordagem desenvolveu-se a partir de técnicas e de instrumentos que permitiram a recolha de informação, nomeadamente a observação participativa, a análise documental, as entrevistas às professoras cooperantes e o teste de avaliação de conhecimento.

Posto isto, o presente estudo ocorreu entre fevereiro e maio de 2018. Tal como se pode verificar pela análise da Figura 1, o mesmo contemplou quatro fases, que foram determinadas pelo problema de investigação, pelas questõesproblema formuladas e pelos objetivos geral e específicos do estudo.

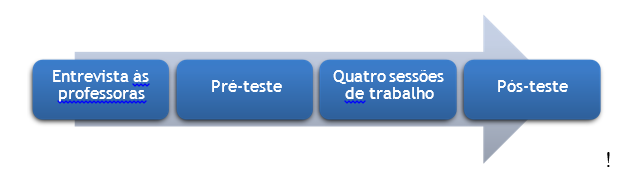
Figura 1 – Sequência-síntese das fases de recolha de dados

 A recolha de dados teve início com a realização de entrevistas às professoras titulares de turma, de forma a se conseguir realizar uma caraterização global dos elementos da amostra.

O teste escrito de avaliação de conhecimentos, preenchido pelos alunos, foi aplicado em dois momentos diferentes: em fevereiro de 2018, a que se chamou Pré-teste, e em maio de 2018, a que se chamou Pós-teste. O teste foi dividido em duas versões e consequentemente realizado em dois momentos do dia: ao início da manhã e ao fim da tarde, devido às caraterísticas do contexto os alunos poderiam desmotivar-se pela quantidade de problemas apresentados em cada teste. Salienta-se que esta estratégia foi utilizada nos dois momentos avaliativos, isto é, no Pré-teste e no Pós-teste. Deste modo, a versão A do teste foi composta por três problemas retirados das provas finais de Matemática do 1.º CEB do 4.º ano. A versão B era composta pelos mesmos problemas matemáticos, mas em termos linguísticos os mesmos sofreram alterações realizadas pelas investigadoras.

Esta opção metodológica surgiu com o intuito de se poder observar a evolução dos alunos da amostra, entre o pré-teste e o pós-teste, após a realização das quatro sessões interventivas, que visavam desenvolver estratégias para decifração e a compreensão dos enunciados dos problemas matemáticos. Por sua vez, com as alterações realizadas entre a versão A e a versão B do teste pretendia-se recolher dados para se analisar a influência da compreensão da leitura e das alterações sintáticas, a partir da interpretação dos enunciados, na realização de problemas matemáticos.

Por fim, realizaram-se as quatro sessões práticas com os elementos da amostra com o intuito de se potenciar o desenvolvimento de estratégias de resolução de problemas e dar a conhecer aos estudantes o método de Polya e das componentes metalinguísticas, método que auxilia a resolução de problemas, podendo contribuir para o sucesso dos estudantes.

Ressalva-se que apesar de se ter usado diversificados instrumentos de recolha de dados, neste artigo só se irá explorar o primeiro e o terceiro problemas do teste de avaliação de conhecimentos, na qual se realizou as alterações semânticas, ou seja, a troca de dados.

2.2. AMOSTRA

A investigação desenvolveu-se em duas escolas do 1.º CEB, pertencentes a um Agrupamento do Porto, colaborando duas turmas do 4.º ano, constituídas na sua totalidade por 31 alunos, com idades compreendidas entre os nove e os onze anos. A seleção dos alunos resultou da participação de todos os elementos da turma, sendo, somente, excluído um caso, nomeadamente um aluno com absentismo regular. Dos 31 alunos, 17 eram do sexo masculino e 14 do sexo feminino. Da totalidade da amostra, somente seis alunos possuíam um diagnóstico de Necessidades Adicionais de Suporte, e nove alunos tinham reprovado alguma vez no seu percurso escolar.

Salienta-se que apesar de os participantes serem provenientes de duas turmas distintas, observar-se-á os dados como sendo um grupo único.

Por sua vez, o estudo também teve a colaboração das professoras titulares de turma, que, a partir da entrevista realizada às mesmas, da análise do Plano Individual do aluno e do Plano da Turma, foi possível caraterizar este grupo como detentor de várias dificuldades em Português e em Matemática, dado que não possuem hábitos de estudo, impossibilitando a consolidação dos conteúdos programáticos. Consequentemente, os elementos da turma também possuíam uma enorme desmotivação perante a escola e a aprendizagem, bem como interesses divergentes a esta, refletindo-se na desconcentração e nos baixos resultados em diversas áreas disciplinares.

2.3. TESTES DE AVALIAÇÃO DE CONHECIMENTO APLICADOS AOS ALUNOS

Tal como referido anteriormente, optou-se por construir um teste composto por duas versões: a versão A era composta por três problemas de provas finais do 1.º CEB e a versão B era constituída pelos três problemas da versão A com alterações linguísticas (Tabela 2). Esta estratégia surgiu visto que as provas finais do 1.º CEB são nacionais, logo estão validadas para o ano de ensino em questão, tendo o intuito de avaliar o modo como os objetivos e as competências essenciais de cada ciclo estão a ser alcançadas pelos alunos no sistema de ensino, assim os professores possam diagnosticar as dificuldades dos alunos e agir em conformidade perante as mesmas.

Desta forma, os problemas selecionados têm em vista o cumprimento dos objetivos delineados para a investigação, sendo problemas verbais que se enquadram no conteúdo de Números e Operações e, ainda, problemas de dois ou mais passos, segundo a classificação de Charles e Lester (1986, citado por Vale & Pimentel, 2004).

Cada problema foi cotado com no máximo cinco pontos, de acordo com os critérios de correção adaptados das provas finais do 1.º CEB.

Salienta-se que para ajudar o tratamento estatístico dos dados obtidos, e apesar de serem os mesmos, rotulou-se os problemas do pré-teste com P1 e P3, e os problemas do pós-teste com PP1 e PP3. Por sua vez, para diferenciar os problemas entre a versão A e a versão B acrescentou-se a respetiva letra, utilizando-se a seguinte nomenclatura: P1A, problema 1 da versão A do pré-teste; P3A, problema 3 da versão A do Pré-teste;P1B, problema 1 da versão B do préteste; P3B, problema 3 da versão B do Pré-teste; PP1A, problema 1 da versão A do pós-teste; PP3A, problema 3 da versão A do Pós-teste; e PP1B, problema 1 da versão B do pós-teste; PP3B, problema 3 da versão B do Pós-teste.

Tabela 2 - Alterações linguísticas nos Problemas1 e 2 – troca da ordem da apresentação dos dados

	Versão A	Versão B
Problema 1	Prova final de Matemática do 1.º CEB de 2015, 1ª fase, 1.º caderno	Alterações semânticas (troca da ordem dos dados)
	O Pedro e a Rita têm, no total, 538 cromos. A Rita tem mais 54 cromos do que o Pedro. Quantos cromos tem o Pedro?	A Rita tem mais 54 cromos do que o Pedro. O Pedro e a Rita têm, no total 538 cromos. Quantos cromos tem o Pedro?
Problema 2	Prova final de Matemática do 1.º CEB de 2015, 2ª fase, 1.º caderno	Alterações semânticas (troca da ordem dos dados)
	O Gil tem 40 filmes. A Lara tem o triplo do número de filmes do Gil. O Mário tem mais 12 filmes do que o Gil e a Lara juntos. Quantos filmes tem o Mário?	O Mário tem mais 12 filmes do que o Gil e a Lara juntos. A Lara tem o triplo do número de filmes do Gil. O Gil tem 40 filmes. Quantos filmes tem o Mário?

A análise das pontuações dos testes de avaliação de conhecimento aplicados aos alunos foi realizada com recurso ao SPSS (Statistics, version 23). Fez-se uma análise quantitativa dos dados recolhidos, no sentido de se tentar encontrar relações entre as variáveis estudadas e, assim, dar-se resposta às questõesproblema.

Para a análise de dados, mais concretamente para a comparação de pontuações médias, antes e depois da intervenção da investigadora (implementação das sessões de trabalho), e entre as pontuações médias obtidas em cada problema, da versão A e da versão B do teste, recorreu-se a testes estatísticos não paramétricos. Não se optou por testes paramétricos, uma vez que estes exigem a verificação da normalidade quando as amostras têm dimensão inferior ou igual a 30 elementos. Apesar da amostra em estudo ser composta por 31 elementos, logo superior a 30, optou-se por uma atitude mais conservadora, atendendo a que este valor se encontra muito próximo do limite que dispensa a aplicação dos testes da normalidade. Assim, recorreu-se ao teste de Wilcoxon, teste não paramétrico para amostras emparelhadas, dado que se recorreu “o mesmo grupo de sujeitos antes e depois de um tratamento ou intervenção” (Pestana & Gageiro, 2008, p. 230).

Optou-se por se trabalhar com um intervalo de confiança de 95%, pelo que o nível de significância foi de 5%, ou seja 0,05. Neste sentido, atendendo a que o “teste de Wilcoxon [se] aplica (…) para analisar diferenças entre duas condições (ex.: préteste-pósteste) no mesmo grupo de sujeitos” (Pestana & Gageiro, 2008, p. 478), considerou-se como hipótese nula a existência de igualdade das médias nos dois momentos em comparação. Assim, se o nível de significância associado ao teste de Wilcoxon (p) for inferior a 0.05, rejeitar-se-á a hipótese nula (H0), pelo que poderemos afirmar com 95% de confiança que os resultados médios em análise são diferentes (Pestana & Gageiro, 2008). 

Para além da análise inferencial no SPSS, realizou-se uma análise descritiva, recorrendo-se à frequência absoluta para observar a frequência de erro cometido pelos elementos da amostra em cada problema, dado que a pontuação alcançada pelos alunos foi o reflexo dos erros cometidos enquanto resolviam os problemas. Para isto, foram construídas tabelas e gráficos com recurso ao Excel.

2.4. APRESENTAÇÃO, ANÁLISE E DISCUSSÃO DOS DADOS

A) DADOS RECOLHIDOS ATRAVÉS DA APLICAÇÃO DO PRÉ- E DO PÓS-TESTE PROBLEMA 1

O problema 1 foi cotado, no máximo com 5 pontos, sendo utilizada uma escala holística, apresentada nos critérios de correção da prova, que dependeria do erro cometido pelos alunos (Apêndice I).

Pré-teste: Versão A vs. Versão B

Ao observar-se os resultados obtidos pelos alunos no Pré-teste entre a versão A e a versão B, verifica-se que a média da versão B foi superior à versão A em 0.10 pontos (1.00 e 1.10 pontos). Apesar do valor das médias ter acrescido, não se pode assumir uma melhoria, uma vez que não podemos rejeitar H0, visto p ser igual a 0.590, isto é, superior a 0.05.

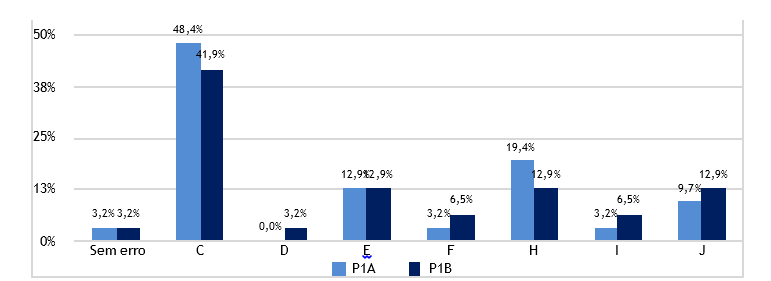
Figura 2 – Percentagem de ocorrência de erros cometidos pelos alunos em P1A e em P1B por tipo de erro

Focando a atenção na Figura 2, observa-se que, maioritariamente, o erro cometido entre nas duas versões do problema foi do tipo C, 48.4% e 41.9%, onde os alunos revelaram alguma compreensão do problema efetuando ou elencando apenas o primeiro passo do problema. Por outro lado, observou-se um decréscimo, entre a versão A e a versão B, de 36.5% no erro H, revelando que existiram menos alunos a adicionarem os 54 cromos, em vez de os subtraírem. Do mesmo modo, observa-se um aumento no erro do tipo I (não responde) e J (apresenta outra resposta), 3.3% e 3.2%, respetivamente, demonstrando a incompreensão do problema ou ausência de resposta.

Pós-teste: Versão A e Versão B

Comparando os resultados obtidos pelos elementos da amostra no pós-teste na versão A e na versão B, verifica-se que houve uma melhoria entre a pontuação média (1.42 e 1.55 pontos). Porém, não se pode assumir uma melhoria significativa estatisticamente, uma vez que não podemos rejeitar H0, visto p ser igual a 0.435, isto é superior a 0.05.

Analisando os erros cometidos na Figura 3, verifica-se que, maioritariamente, o erro cometido nas duas versões foi novamente do tipo C, onde os alunos revelam alguma compreensão do problema, efetuando ou elencando o primeiro passo do problema, nomeadamente subtrair 54 aos 538 cromos, tendo aumentado 6.5% no PP1B. Por outro lado, observou-se um aumento de 3.3% na resposta totalmente correta e nos erros do tipo H, adiciona 54 aos 538 cromos, e J, apresenta outra resposta, demonstrando a total incompreensão do problema por parte dos alunos.

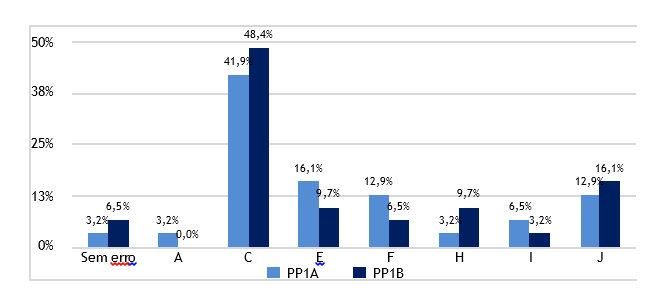
Figura 3 - Percentagem de ocorrências de erros cometidos pelos alunos em PP1A e em PP1B por tipo de erro

Pré-teste vs. Pós-teste: Versão A

Observando as médias obtidas na versão A em ambos os momentos avaliativos, verifica-se que no pós-teste os elementos da amostra obtiveram uma pontuação mais elevada comparando com o Pré-teste (1.00 e 1.42 pontos). No entanto, visto p ser igual a 0.800, superior a 0.05, não se pode rejeitar H0.

Tendo em conta os erros que os alunos cometeram neste problema nos dois momentos avaliativos (Figura 4), o erro mais comum foi o tipo C, subtrair 54 aos 538 cromos, resolução na qual os alunos demonstram alguma compreensão do problema, realizando ou elencando a primeira fase do mesmo. Por outro lado, observa-se uma melhoria de um aluno que após a realização do pós-teste apresentou só um pequeno erro de cálculos, erro A.

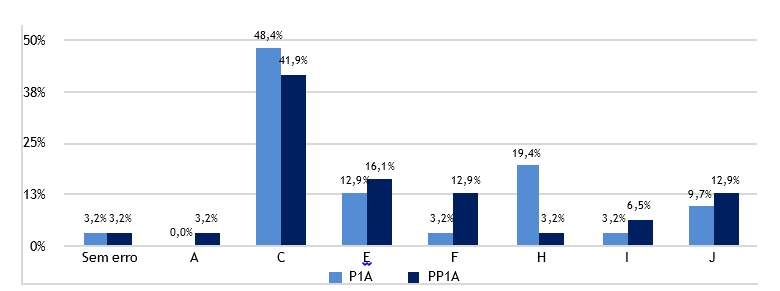
Figura 4 - Percentagem de ocorrências de erros cometidos pelos alunos em P1A e em PP1A por tipo de erro

Salienta-se a estratégia utilizada por um aluno (Figura 5), sendo que, apesar de não ter a pontuação máxima devido a se ter enganado na primeira fase do problema, adicionando em vez de subtraindo, se verifica um ótimo conhecimento matemático e um desenvolvimento do cálculo mental, uma vez que o aluno utilizou a decomposição de números para resolver o problema.

 

Figura 5 - Estratégia desenvolvida por um aluno no P1A

Pré-teste vs. Pós-teste: Versão B

Comparando as pontuações obtidas na versão B entre os dois momentos avaliativos, observa-se que a média foi superior na versão B, existo uma pequena melhoria (1.10 e 1.55 pontos). O valor do nível de significância foi de p ser igual a 0.047, inferior a 0.05, o que leva à rejeição da H0. 

De forma a entender quais os erros cometidos pelos alunos, por não terem atingido a pontuação máxima, analisar-se-á a Figura 6. Assim, verifica-se que o maior erro cometido nos dois momentos avaliativos foi o erro C, 41.9% e 48.4%, demonstrando alguma compreensão e interpretação do problema uma vez que elenca o primeiro passo da resolução. Por outro lado, apesar de terem diminuído os erros do nível de desempenho mais baixo H e I, nomeadamente adicionar 54 cromos à totalidade e não responder, acresceu 3.2% no erro J, demonstrando, que no segundo momento avaliativo, 16.1% (seis) dos alunos apresentaram uma resposta completamente díspar ao que é solicitado.

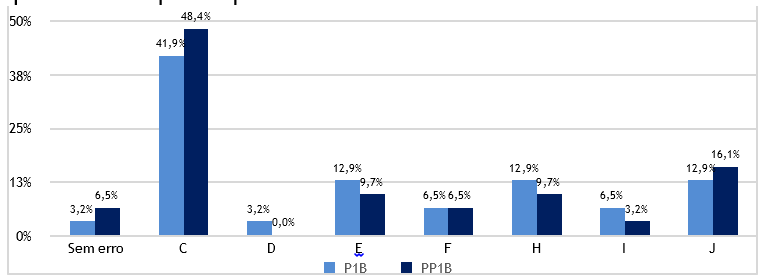
Figura 6 - Percentagens de ocorrências de erros cometidos pelos alunos em P1A e em PP1A por tipo de erro

2.4.1.2. Problema 3

O problema 3 foi cotado com o máximo de 5 pontos e recorreu-se a uma escala analítica apresentada nos critérios de correção da prova final do 1.º CEB de 2015, 2ª fase, podendo ser atribuído entre 0 e 5 pontos dependendo do erro cometido (Apêndice II).

Pré-teste: Versão A vs. Versão B.

Comparando os resultados obtidos pelos alunos no problema 3, no pré-teste entre a versão A e a versão B, observa-se uma descida das médias dos elementos da amostra (2.61 e 2.16 pontos). Apesar do valor das médias das respostas corretas ser distinto, não se pode assumir uma relação entre as duas versões, uma vez que não podemos rejeitar H0 visto p ser igual a 0.245, isto é, superior a 0.05.

Centrando-se a atenção nos tipos de erros cometidos pelos alunos na resolução do problema 3 entre a versão A e a versão B (Figura 7), observa-se um decréscimo de 12.9% em P3B nos alunos que o realizarem sem qualquer erro, e um aumento de ocorrências dos erros B, que apresenta uma estratégia apropriada e completa, mas comete um pequeno erro de cálculo e reponde de acordo com o erro cometido, e C, apresenta uma estratégia adequada, porém não inclui o número de filmes do Gil. Por outro lado, verifica-se um aumento de ocorrências do erro G, que decorre da ausência de resolução. Salienta-se que um aluno não resolveu o problema por não saber o significado de triplo, demonstrando a dificuldade destacada pelas professoras titulares nas respetivas áreas de saber.

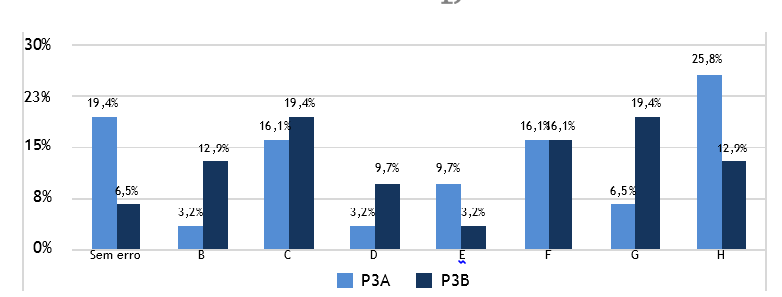
Figura 7 - Percentagens de ocorrência de erros cometidos pelos alunos em P3A e em P3B por tipo de erro

Pós-teste: Versão A vs. Versão B

Os resultados obtidos pelos alunos no problema 3 desceram ligeiramente, aquando comparando as duas versões (3.55 e 3.451 pontos). Apesar do valor das médias ser distinto, não se pode assumir uma relação entre as duas versões, uma vez que não podemos rejeitar H0 visto p ser igual a 0.400, isto é, superior a 0.05.

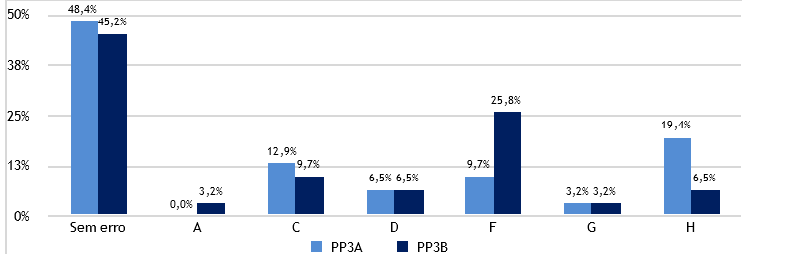
Figura 8 - Percentagem de ocorrências de erros cometidos pelos alunos em PP3A e em PP3B por tipo de erro

Na Figura 8, observa-se os erros cometidos em PP3A e em PP3B, no qual 48.4% no PP3A e 45. 2% no PP3B realizaram o problema sem cometer nenhum erro. Salienta-se o aumento de 16.1% de ocorrências do erro tipo F, tendo respondido 52, isto é, adicionaram o número de filmes do Gil aos do Mário sem calcular os filmes da Lara, demonstrando que não compreenderam o problema na sua plenitude. Por outro lado, ocorreu um decréscimo de 12.9% nas ocorrências do erro H, mostrando que os alunos compreenderam algum passo do problema, uma vez que este valor, 12,9%, foi distribuído pelos outros erros.

Pré-teste vs. Pós-teste: Versão A

Ao analisar-se as médias obtidas na versão A entre os dois momentos avaliativos, verifica-se uma subida de 0.94 do pré-teste para o pós-teste (2.61 e 3.55 pontos). O teste de Wilcoxon tem um nível de significância de 0.050, o que leva à rejeição da H0, pelo que se pode concluir que os resultados obtidos pelos alunos são diferentes nos dois momentos avaliativos. Observando-se a Figura 9, comprova-se a melhoria dos alunos sem nenhum erro no segundo momento avaliativo, existindo um acréscimo de 26%. Por este motivo, observa-se um decréscimo na ocorrência da maioria dos erros em PP3A, exceto na ocorrência do erro D que aumentou 3.3% (um aluno), sendo que estes alunos calcularam corretamente o número de filmes da Lara, fase de maior pontuação, e não calcularam o número total de filmes.

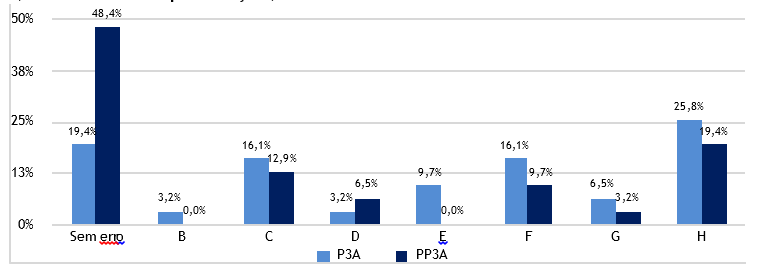
Figura 9 - Percentagem de ocorrências de erros cometidos pelos alunos em P3A e em PP3A por tipo de erro

Pré-teste vs. Pós-teste: Versão B

Comparando as médias obtidas pelos elementos da amostra na versão B nos dois momentos avaliativos, averigua-se que houve uma melhoria no pós-teste (2.16 e 3.45 pontos). O teste de Wilcoxon tem associado um nível de significância de 0.001, inferior a 0.05, o que leva à rejeição de H0, concluindo-se que os resultados obtidos pelos alunos são diferentes nos dois momentos de avaliação.

Observando-se a Figura 10, averigua-se um acréscimo acentuado, 38.7%, na realização do problema totalmente correto, o que, consequentemente, permitiu um decréscimo da ocorrência dos restantes tipos de erros, exceto do erro F, os alunos respondem 52, isto é, calculam o número de filmes que o Gil possui, não determinando o número total de filmes. O acréscimo na ocorrência deste erro permite verificar que 25.8% dos alunos não conseguiu compreender parte do enunciado do problema, ultrapassando fases primordiais da resolução.

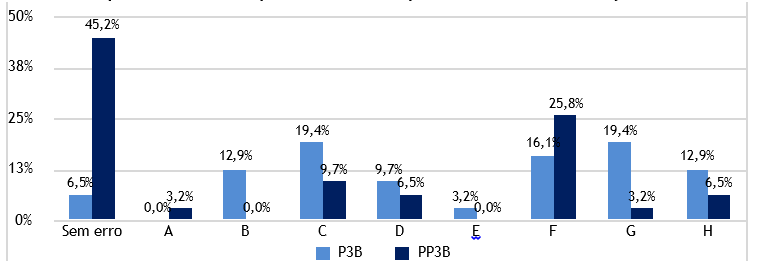
Figura 10 - Percentagem de ocorrência de erros cometidos em P3B e em PP3B por tipo de erro

2.4.2. Dados recolhidos através da aplicação de instrumentos de natureza qualitativa

Refletindo-se sobre a observação direta e a análise documental, verifica-se que, durante a ação da investigadora, os alunos conseguiram compreender o método de Polya e apropriar-se das suas fases. A desmotivação, referenciada pelas professoras titulares de turma durante a entrevista, transformou-se no gosto em querer conhecer mais, desafiando-se uns aos outros para verem quem conseguia resolver o problema de uma estratégia diferente e quem conseguia alcançar o resultado certo e mais rápido.

Posto isto, pode-se observar que os alunos adquiriram as estratégias desenvolvidas durante a exploração das fases do método de Polya articulado com a compreensão leitora do aluno, uma vez que quando realizaram o Pós-teste estiveram sempre presentes (Figura 11).

Figura 11 - Estratégias desenvolvidas ao longo das sessões de trabalho e aplicadas por um aluno no PP2B

CONCLUSÕES

 A partir da apresentação e da análise dos dados recolhidos elaboraram-se as conclusões que podem originar um novo ciclo investigativo. Essas conclusões foram concebidas através da análise dos objetivos e da problemática de base. Posto isto, os resultados obtidos, comparando a versão A e B, nos problemas apresentados e com este grupo de elementos da amostra, não permitem averiguar que as alterações semânticas, resultantes nos enunciados da versão B, influenciam a resolução de problemas, dado que não se obteve significância estatística.

No entanto, quando comparamos os resultados obtidos nos dois momentos avaliativos, pré-teste e pós-teste, os alunos já conseguiram alcançar resultados superiores no pós-teste, podendo-se afirmar a partir da aplicação do teste de Wilcoxon, com 95% de confiança, que as sessões concretizadas com as duas turmas, permitiram uma evolução na compreensão da resolução de problemas. Esta evolução denota que o conhecimento do método de Polya, articulado com a compreensão leitora e de diversificadas estratégias de resolução de problemas, motivou os alunos para a aquisição de conhecimento e, consequentemente permitiu uma melhor prestação, resultante da compreensão das fases e das estratégias desenvolvidas ao longo da resolução de um problema matemático.

A análise documental permitiu observar que os alunos, ao procederem às estratégias metalinguísticas, conseguiram compreender rapidamente o que solicitado nos problemas com enunciados verbais. Por sua vez, quando comparado o tipo de erro de cada problema verificou-se uma melhoria na resolução do problema, demonstrando alguma influência do Português na resolução de problemas, apesar de não se ter obtido significado estatístico.

Ressalva-se que sendo o Português o veículo de comunicação entre cidadãos portugueses, em Portugal, é urgente que os atuais e futuros agentes educativos, os professores, reflitam sobre a necessidade de um ensino articulado entre as áreas curriculares de Matemática e Português.

REFERÊNCIAS

Baptista, A. (Ed.) (no prelo). Leitura, compreensão e usabilidade dos problemas de matemática com textos bimodais mistos. Porto: Edições Afrontamento. ISBN 978-972-36-1540-1.

Carmo, H. & Ferreira, M. (2008). Metodologia da Investigação – Guia para Autoaprendizagem. Lisboa: Universidade Aberta.

Choupina, C. (no prelo). Particularidades textuais dos problemas de Matemática no design de uma investigação sobre leitura. In A. Baptista (Ed.). Leitura, compreensão e usabilidade dos problemas de matemática com textos bimodais mistos. Porto: Edições Afrontamento. ISBN 978-972-36-1540-1. Capítulo IV. 

Correia, D. (2003). Estudos experimentais sobre leitura e compreensão de problemas verbais de matemática. Tese de Doutoramento. Faculdade de Letras, Lisboa, Portugal.

Martins, G., Gomes, C., Brocardo, J., Pedroso, J., Carrilho, J., Silva, L., Encarnação, M., Horta, M., Calçada, M., Nery, R., & Rodrigues, S. (2017). Perfil dos alunos à saída de escolaridade obrigatória. Lisboa: Mistério da Educação/Direção Geral de Educação. ISBN: 978 972 742 416 0.

Mascarenhas, D., Maia, J., & Martínez, T. S. (2017). Geometria e Grandezas no 5.º ano: Dificuldades e Estratégias – Um Estudo em duas escolas do distrito do Porto. Berlin: Novas Edições Académicas. ISBN: 978-620-2-40050-3.

Máximo-Esteves, L. (2008). Visão panorâmica da investigação-acção. Porto: Porto Editora.

Monteiro, I. (2018). No futuro se faz presente. Relatório de estágio apresentado à Escola Superior de Educação do Politécnico do Porto, Portugal. Disponível em: http://recipp.ipp.pt/handle/10400.22/12162

Ӧsterholm, M. (2006). A Reading comprehension perspective on problem solving. Linkӧnping University: Department on Mathematics.

Ӧsterholm, M. (s.d.). Characterizing Reading comprehension of mathematical texts. Linkӧnping University.

Pacheco, J. (1995). Da componente nacional às componentes curriculares regionais e locais. Lisboa: Ministério da Educação.

Pestana, M. H. & Gageiro, J.N. (2008). Análise de dados para ciências sociais: A complementaridade do SPSS. Lisboa: Edições Sílabo.

Pires, S. (2004). Da compreensão verbal à resolução de problemas: O Português na aula de Matemática. Dissertação de Mestrado, Universidade do Algarve, Algarve, Portugal.

Polya, G. (1977). A arte de resolver problemas. Rio de Janeiro: Editora Interciência.

Sá, A., Sousa, C., Oliveira, D., Cunha, I., Saleiro, J., Carneiro, L. & Silva, N.

(2006). Problemas: Estratégias de resolução de problemas. In D. Fernandes (Coords.), Viajar na Matemática: Programa de formação contínua em matemática para professores do 1.º Ciclo do Ensino Básico, 1-43. Porto: Escola Superior de Educação do Instituto Politécnico do Porto.

Stival, J. & Lisbôa, A. (2014). A interpretação da linguagem matemática e da Língua materna: Uma arte na resolução de problemas. Os desafios da escola pública Paranaense na prespectiva do professor PDE, (Online), 1.

UNESCO (1990). Declaração Mundial sobre Educação para Todos: Satisfação das necessidades básicas de aprendizagem. Jomtien: UNESCO. 

UNESCO (2000). Educação para todos: O compromisso de Dakar (2ª ed). Brasília: UNESCO, CONSED.

Vale, I. & Pimentel, T. (2004). Resolução de problemas. In P. Palhares (Coords.).

Elementos de Matemática para professores do Ensino Básico. Lisboa: LIDEL.

Valentin, J. & Sam, L. (2004). Roles of semantic structure of arithmetic word problems on pupils ability to identify the correct operation. University of Science Malaysia.

Viana, F., Ribeiro, I., Fernandes, I., Leitão, C., Gomes, S., Mendonça, S., & Perreira, E. (2010). O ensino da compreensão leitora. Da teoria à prática pedagógica: Um programa de intervenção para o 1.º Ciclo do Ensino Básico.

Coimbra: Edições Almedina S.A.

APÊNDICES APÊNDICE I: TIPOLOGIA DE ERRO NO PROBLEMA 1

Tabela 3 - Descrição do tipo de erros cometidos pelos alunos no problema 1

Tipo de erro	Descrição do erro cometido
A	Resolve corretamente, usando uma estratégia apropriada e completa, mas não apresenta a resposta.
B	Apresenta uma estratégia apropriada e completa de resolução do problema, mas apresenta uma resposta incorreta.
C	A resposta revela alguma compreensão dos dados do problema. 538-54, independentemente, de realizar ou não a operação.
D	Responde corretamente, sem apresentar uma explicação adequada, ou sem apresentar uma explicação.
E	Responde apenas 269.
F	Responde: 538! ÷2=269 269! −54=215 Apresenta uma estratégia apropriada e completa de resolução do problema, mas inverta a ordem da sua aplicação.
G	Responde: 538! ÷2=269 269! +54=323
H	Responde: 538! +54=592
I	Não responde.
J	Apresenta outra resposta.

APÊNDICE II: TIPOLOGIA DE ERRO NO PROBLEMA 3

Tabela 4 - Descrição do tipo de erros cometidos pelos alunos no problema 3

Tipo de erro	Descrição do erro cometido
A	Responde corretamente, sem apresentar uma explicação adequada, ou sem apresentar uma explicação.
B	Apresenta uma estratégia apropriada e completa de resolução do problema, mas comete um pequeno erro de cálculo e responde de acordo com o erro cometido.

 

C	Responde: 40 x 3 e, de seguida, adiciona 12. Apresenta uma estratégia apropriada de resolução do problema, mas não inclui, na sua resposta, o número de filmes que o Gil tem.
D	Responde: 40! ×3=120 O aluno determina corretamente o número de filmes da Lara, não determinando o número total de filmes.
E	Responde: 160 O aluno determina corretamente o número de filmes da Lara e do Gil juntos, mas não determina o número de filmes dos três amigos.
F	Responde: 52 O aluno determina corretamente o número de filmes que o Gil tem, não determina o número de filmes da Lara, mas refere que o número de filmes do Mário é 40+12=52.
G	Não responde.
H	Apresenta outra resposta.