Artigo Completo

As tecnologias de apoio ao conhecimento

Matemático: uma experiência no 2.º CEB

António Figueiredo

Escola Básica Padre António Luís Moreira

Cláudia Lima

Escola Superior de Educação do Politécnico do Porto

Ângela Couto

Escola Superior de Educação do Politécnico do Porto

Resumo

A educação matemática atual enfatiza a dinâmica proativa do professor e a participação ativa do aluno nas dinâmicas de sala de aula, num processo em que o professor, sendo um facilitador das aprendizagens, pode apoiar o aluno na construção de representações matemáticas profícuas e profundas, transferindo-lhe gradualmente o controlo da qualidade das suas aprendizagens. Esta perspetiva de trabalho exige, claramente, por parte dos professores, coragem na rutura com as metodologias de ensino tradicionais. Neste estudo, e ao longo de um ano letivo, desenvolveram-se estratégias diversificadas e utilizaram-se recursos tecnológicos variados na abordagem da Geometria a um conjunto de 39 alunos do 5.º ano de escolaridade. Este é um tópico recheado de terminologia específica, de propriedades e relações entre objetos geométricos, de teoremas, numa lógica de matemática pura, que dificulta a sua aprendizagem por parte dos alunos. A referida abordagem permitiu que estes alunos se envolvessem autonomamente nas descobertas, nas aprendizagens e na autoavaliação dos seus conhecimentos. Desta forma, também se potenciou o direito e acesso às mesmas oportunidades de aprendizagem, na verdadeira aceção de escola inclusiva, que respeita as características idiossincráticas de cada um, diminui as desigualdades e dá preferência à compreensão em vez da memorização a curto prazo.

Palavras-chave: tecnologia, aprendizagem, geometria, escola inclusiva.

Abstract

The current mathematical education emphasizes the active participation of students in the classroom dynamics, in their interactions, in a process in which the teacher, being a facilitator of the learning, can support the student in the construction of proficient and deep mathematical representations, gradually transferring control of the quality of their learning. This perspective of work clearly requires, on the part of the teachers, courage in the rupture with the traditional teaching methodologies. In this study and throughout a school year, diverse strategies were developed and various technological resources were used in the approach of Geometry to a set of 39 students of the 5th school year. This topic, filled with specific terminology, properties and relations between geometric objects, of theorems, in a logic of pure, abstract mathematics, which hinders students' learning, with the said approach, allowed a great implication on the part of the students, discoveries, learning and self-assessment of knowledge. In this way, the right to and access to the same learning opportunities, in the true meaning of an inclusive school, which respects the idiosyncratic characteristics of each one, diminishes inequalities and gives preference to understanding instead of short-term memorization.

Keywords: technology, learning, geometry, inclusive school.

INTRODUÇÃO

A escola do séc. XXI tem de se adaptar às novas solicitações da sociedade, da comunidade educativa de que faz parte, criando condições para ensinar alunos com diferentes interesses, motivações e capacidades. Ou seja, ensinar todos, dando resposta à diversidade, tornando-se num local estimulante em termos cognitivos e socioafetivos, ensinando a pensar e a aprender.

O apelo à memorização a tempo curto e a formas convencionais de pensamento, a algoritmos ou procedimentos que se decoraram sem se compreender, entregou a matemática a um caminho que afugenta muitos alunos e os condena ao fracasso. No caso particular da Geometria, a situação ainda assume contornos de maior gravidade pela forma como é feita a sua abordagem, muitas vezes recorrendo à Álgebra que é, para muitos autores (e.g., Almeida, 1994; Maia & Couto, 2014; Maia-Lima, 2016), uma conexão que prejudica gravemente a capacidade de refletir sobre os objetos geométricos e compreender as suas relações.

Os programas de Geometria dinâmica podem ser um suporte fundamental para que os alunos façam as suas próprias descobertas, reconheçam propriedades e relações entre os objetos, descubram teoremas, ou seja, sejam ativos no seu próprio processo de aprendizagem. A capacidade de abstração que frequentemente se exige na abordagem da Geometria não está acessível a todos os alunos relevando este tópico para um patamar de dificuldade crescente que dificilmente poderá ser ultrapassado. Desta forma, ensinar terá que passar por um trabalho cooperativo envolvendo todos os professores e basear-se no estudo dos aprendentes, no que concerne a emoções, memória e desempenho intelectual. Ensinar na escola de massas implica a implementação de uma prática pedagógica que privilegie a investigação permanente.

Avaliar as competências adquiridas em Matemática será procurar saber se os objetivos previamente estabelecidos, como desejáveis, foram alcançados no seu sentido mais lato, ou seja, se os alunos são capazes de incorporar, criar, melhorar e aplicar o conhecimento adquirido em novos desafios.

1. UMA METODOLOGIA ATIVA PARA O ENSINO DA MATEMÁTICA

Nos dias de hoje a educação enfrenta enormes desafios que obrigam o professor, enquanto mediador da criação de novo conhecimento no aluno, a repensar novas formas de atuar. O paradigma transmissivo, ainda muito presente nas nossas salas de aula, não responde às necessidades de cada aluno, pois ensina a todos como se fossem um só, reduzindo, portanto, e para muitos, a possibilidade de sucesso, bem como vê a motivação e o interesse dificultados, acrescida pelo caráter multidisciplinar do currículo escolar. Para além destes aspetos, a desconexão com a realidade daquilo que se ensina, e o nível de abstração da Matemática que frequentemente se impõe, não permite aos alunos mais novos vislumbrar a sua utilidade no presente, nem no futuro. Permite, apenas, que a informação se traduza num conjunto de procedimentos, técnicas, factos, conceitos e relações num permanente apelo à memória por não serem compreendidas. O Plano Nacional de Promoção do Sucesso Escolar, aprovado em Conselho de Ministros em 2016, tem, assim, “o objetivo de melhorar as práticas educativas e as aprendizagens dos alunos” (Conselho de Ministros, p. 1195) de forma “a garantir uma educação de qualidade como resposta às novas exigências de uma sociedade do conhecimento e da competitividade” (idem). Este plano refere, ainda, a importância de medidas não remediativas mas de “desenvolvimento de estratégias inovadoras e indutoras de mudança” (Conselho de Ministros, p. 1196). Deste modo,

um dos principais objetivos da educação é aumentar a motivação dos alunos para alcançar uma aprendizagem significativa [e] a utilização de tecnologias nas salas de aula com as quais os alunos estão familiarizados, tais como o smartphone ou o tablet, é uma forma de atingir esse objetivo (Prieto, Palma, Tobías & Léon, 2019, p. 1).

No caso particular dos conteúdos de Geometria, presentes no programa de Matemática homologado em 2013 e ainda em vigor para o 5.º ano de escolaridade, realça-se o facto de estar recheado de simbolismos, de terminologia específica, de propriedades e relações entre objetos geométricos, de teoremas, numa lógica de matemática pura, abstrata, que dificulta a sua aprendizagem. E, assim,

a capacidade de aprendizagem, enquanto aquisição de formas convencionais de pensamento e de memorização, tantas vezes superada pelas novas tecnologias, afiguram-se, se não obsoletas, pelo menos claramente insuficientes perante a necessidade de encontrar respostas inovadoras para os diversos desafios tecnológicos, científicos, artísticos e morais, dos nossos tempos (Sternberg & Lubart, 1991, 1996, citado por, Candeias & Almeida, 2007, p. 523).

Os benefícios da utilização de recursos tecnológicos modernos (dispositivos móveis, softwares de geometria dinâmica, plataformas tecnológicas, etc.) para promover aprendizagens duradouras e com significado são apresentados por vários autores (e.g., Bennison & Good, 2010; Bishop, Hart, Lerman & Nunes, 1993; Maia & Couto, 2014; Olive & Makar, 2010), bem como o recurso à gamificação como estratégia de motivação nessa construção de saberes por parte do aluno, à luz da abordagem socioconstrutivista (Buckley & Doyle, 2014; Prieto et al., 2019; Sakai & Shiota, 2016; Seixas, Gomes & De Melo Filho, 2016).

1.1. O GEOGEBRA NA SALA DE AULA

A revolução tecnológica em que vivemos determina preparar alunos para uma sociedade cognitiva em que se exige mais conhecimento, criatividade e inovação. Tal como refere Fonseca (1998), “ensinar a pensar e aprender a ser inteligente deverão constituir os objetivos preferenciais dos sistemas de educação modernos” (p. 280). Por isso, os computadores e os dispositivos móveis, presentes na vida de todos nós, devem, também, de fazer parte da sala de aula do séc. XXI. O aluno tem que ser competente nesta área, daí a urgência numa mudança da realidade pedagógica-didática nas salas de aula, alterando o paradigma da transmissão do conhecimento pelo paradigma da descoberta, da construção do conhecimento. O aluno tem de ser capaz de produzir o seu próprio conhecimento, refletindo, ter espírito crítico, tornando-se cada vez mais autónomo, preparar-se para ser um indivíduo que possa atuar na sociedade do futuro.

Na conceção de uma escola para todos, a escola inclusiva, que respeita as características idiossincráticas de cada um, diminui as desigualdades e dá preferência à compreensão em vez da memorização a curto prazo. Esta escola questiona as abordagens descontextualizadas e enfraquecidas de conexões que podem condenar muitos alunos ao insucesso escolar. Neste aspeto, em contexto de sala de aula, a tecnologia poderá ser um meio de sucesso na relação pedagógica entre professor e aluno, pois o professor tentará responder às necessidades individuais de todos e de cada um, organizando a aprendizagem e estimulando o seu desenvolvimento cognitivo e socio-afetivo (Livingstone, 2012; Maia & Couto, 2014).

O software de geometria dinâmico, Geogebra, ao permitir que o aluno aprenda fazendo, experimentando e manipulando, contribui para a diminuição dos mecanismos de memorização em prol da compreensão das relações e conexões entre objetos geométricos. Com este programa é possível, de um modo rápido, testar conjeturas, fazer demonstrações, confirmar propriedades geométricas e manipular construções, sem que estas percam as suas caraterísticas.

Neste estudo, utilizou-se o Geogebra para a exploração de conteúdos matemáticos de geometria de 5.º ano, o que permitiu aos alunos refletirem, tirarem as suas próprias conclusões, compreendendo melhor os conceitos e as relações geométricas, numa dinâmica de sala de aula em que a comunicação matemática, na exploração de guiões de exploração, é muito favorecida. Ponte e Canavarro (1997) também defendem que “é através da comunicação matemática que os alunos tomam consciência dos processos de construção e validação do conhecimento matemático, que aprendem as razões que fazem com que algo tenha ou não sentido, seja ou não verdade em matemática” (p. 111).

1.2. GAMIFICAÇÃO

O acesso à internet, quer de forma particular quer através de redes wireless, partilhadas por entidades públicas e privadas, inclui, neste momento, um número significativo de escolas, o que permite utilizar esta grande teia de informação e recursos que são, hoje, imprescindíveis aos jovens e mesmo às crianças.

Um estudo do Instituto Nacional de Estatística (INE), de 2016, refere que 96% dos agregados familiares com crianças têm acesso à internet, 94% têm acesso à banda larga e que, em ambos os casos, as percentagens têm vindo a crescer nos últimos anos. Aliás, este estudo indica que o acesso à internet em mobilidade duplicou nos últimos quatro anos (2012 a 2016) e que o acesso privilegiado para se aceder à internet é através do telemóvel/smartphone, com maior percentagem do que o próprio computador portátil.

Outro estudo, de Simões, Ponte, Ferreira, Doretto e Azevedo (2014), apresenta os resultados nacionais do projeto Net Children Go Mobile, onde refere que Portugal se encontra acima da média europeia no que concerne à percentagem de escolas com rede wifi e, também, que o jogo é a atividade diária referida por um terço dos internautas portugueses. Assim, como refere Prieto et al. (2019), “a inclusão de cenários apoiados por jogos e competição aumenta a participação ativa dos alunos” (p. 1). Neste contexto, o termo gamificação tem ganho não só destaque, como muitos adeptos entre professores e alunos, pois permite raciocinar numa dinâmica de jogo e envolver o público na resolução de problemas pelo caráter da competição, de mecanismos de recompensas (Ghamdi & Holland, 2016), da mudança de comportamento e de ainda ser, hoje, uma inovação (Burke, 2014). Aliando o efeito descrito que os jogos podem ter nos alunos à necessidade de o professor obter evidências do processo de aprendizagem de cada um (Prieto et al., 2019), aqueles são aliciados para a utilização de plataformas como o Kahoot e o Plickers. Estas duas plataformas, como outras igualmente conhecidas, permitem a apresentação de um conjunto questões com feedback imediato sobre as suas respostas. O Kahoot exige que cada interveniente tenha o seu próprio telemóvel com acesso à internet para poder responder; no caso do Plickers é necessário apenas um telemóvel, o do professor por exemplo, para recolher as respostas dos alunos através da leitura de QR Codes em cartões de resposta. Apesar de estimular a participação e o interesse dos alunos, este tipo de gamificação permite, essencialmente, testar conhecimentos adquiridos, apelando à memória e recolhendo uma resposta. De realçar que, com estes recursos dificilmente se produz desenvolvimento intelectual, de cognição, enquanto processo de aquisição de conhecimentos.

2. METODOLOGIA

Neste estudo adotou-se uma metodologia de investigação-ação participativa e na qual se combinaram técnicas de recolha de dados de natureza qualitativa

(observação direta, produções dos alunos, diário de bordo) e quantitativa (inquéritos por questionário). O estudo desenvolveu-se ao longo do ano letivo de 2017/18, durante os segundo e terceiro períodos, no qual foram implementadas várias tarefas, algumas delas, envolvendo recursos e plataformas tecnológicas para a aprendizagem de conteúdos de Geometria, previstos no programa de Matemática do 5.º ano de escolaridade. Iniciou-se o ciclo de sessões com a utilização, unicamente, dos instrumentos de desenho e terminou-se sem a utilização de qualquer recurso para além do caderno. Nas sessões intermédias implementaram-se atividades envolvendo o Geogebra, o Kahoot e o Plickers. No final do ciclo de propostas com o Geogebra, das duas sessões com o Kahoot, da sessão do Plickers e, das primeira e última sessões, aplicou-se um inquérito por questionário que continha quatro questões:

- Gostaste da forma como os conteúdos foram tratados nesta aula?
- Nesta aula estiveste envolvido nas tarefas?
- Achas que, o desenhar figuras geométricas e fazer o registo no caderno diário (ou o Geogebra/Kahoot/Plickers) te pode ser útil para aprender matemática?
- Se tivesses que fazer uma apreciação (um comentário) sobre esta aula, o que dirias?Nas sessões com recurso ao Geogebra, os alunos faziam as suas próprias descobertas, tiravam conclusões, conjeturavam e, algumas destas conjeturas, resultavam nos teoremas previstos no programa de Matemática para o 5.º ano de escolaridade. Todas as 15 sessões com este software foram acompanhadas por 10 guiões de exploração autónoma nos quais, através de um conjunto de questões de orientação, os alunos iam respondendo, tiravam conclusões e organizavam as descobertas e as aprendizagens num dossier digital. Os vários guiões (G) tinham como objetivo: (G1) conhecer e explorar o Geogebra, pontos, retas e circunferências; (G2) posição relativa de retas no plano; (G3) propriedades dos ângulos verticalmente opostos, conjeturar; (G4) ângulos alternos internos e suas respetivas propriedades em retas paralelas; (G5) ângulos alternos externos; (G6) ângulos correspondentes; (G7) soma das amplitudes dos ângulos internos de um triângulo, relação entre a amplitude de um ângulo externo de um triângulo e a soma das amplitudes dos ângulos internos não adjacentes; (G8) explorar e demonstrar no Geogebra, triângulos equivalentes; (G9) paralelogramos, lados do paralelogramo, amplitude dos ângulos internos do paralelogramo, diagonais do paralelogramo; (G10) critérios de igualdade de triângulos.
A observação direta do trabalho que o aluno desenvolvia, permitia ao professor ter uma perceção complementar das competências adquiridas. Com o Kahoot e o Plickers previa-se uma avaliação formativa das abordagens anteriormente feitas, como uma forma de consciencializar, cada aluno, das suas eventuais dificuldades e informar o professor da necessidade, ou não, de medidas de apoio adicionais a conteúdos ou a determinados alunos. Portanto, o Geogebra, por um lado, e o Kahoot e o Plickers, por outro, eram recursos que se complementavam nos objetivos máximos para os quais eram utilizados.
Este inquérito procurava conhecer a perceção dos alunos em relação às potencialidades do recurso utilizado para o seu processo de aprendizagem e, portanto, a questão III ia variando conforme a estratégia utilizada.

2.1. OS PARTICIPANTES

O grupo de participantes neste estudo era constituído por 39 alunos do 5.º ano, de duas turmas (A e B) de uma escola do Distrito do Porto. A turma A era claramente distinta da turma B em diversos aspetos, quer de comportamento, quer de participação e interesse na vida escolar, quer ao nível das expetativas e do acompanhamento familiar.

Os alunos da turma A, na sua generalidade, eram organizados, responsáveis, confiantes, participativos, e com comportamentos adequados ao ambiente de aprendizagem. Apresentavam grande empenho para obterem sucesso académico a um nível mais elevado sustentado por um background familiar estável e, com os encarregados de educação (EE), a acompanhar, de perto, este percurso. Nesta turma de 20 alunos existiam apenas três alunos com um acompanhamento mais próximo, devido às dificuldades ao nível do seu desempenho cognitivo.

No que concerne à turma B (19 alunos), apenas seis alunos se podiam comparar à generalidade dos da turma A. Os restantes requeriam acompanhamento permanente para progredirem na aprendizagem ao nível da turma A. No geral eram alunos pouco interessados, desorganizados, com comportamentos perturbadores, apresentando dificuldades na aquisição de conhecimentos. Ao nível do agregado familiar, 60% das famílias tinham direito a subsídios de apoio do estado e o acompanhamento do percurso escolar dos seus educandos era muito deficitário, havendo seis EE desta turma que raramente iam à escola. Um dos alunos estava institucionalizado por determinação judicial, outro apresentava problemas psicológicos.

No aproveitamento académico do 5.ºA, como se pode ver na Figura 1, não havia nenhum aluno com nível negativo e verificou-se uma melhoria na comparação dos resultados obtidos no 3.º período do 4.º ano de escolaridade e o 1.º período do 5.º ano. Estas evidências são visíveis pela diminuição do número de níveis Suficiente e pelo aumento do número de níveis Bom. Apesar das características da turma do 5.º B, do 4.º ano para o final do primeiro período do 5.º ano, verificou-se, também, que metade dos alunos que estavam no nível medíocre subiu para suficiente e bom (ver Figura 1).

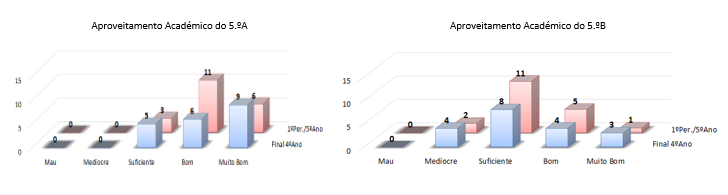
Figura 1 - Desempenho Académico dos Alunos das Turmas Estudadas

2.2. RESULTADOS

Neste estudo procurou-se, fundamentalmente, perceber o interesse e o desempenho cognitivo dos alunos na construção do saber, em matemática, utilizando as tecnologias.

Quer na sala de aula mais tradicional, quer na sala de informática, procurouse ajudar os aprendentes na eliminação de obstáculos e nos seus processos de construção do seu conhecimento.

Na primeira sessão do estudo, numa aula mais tradicional, abordaram-se as propriedades de triângulos e os paralelogramos utilizando os instrumentos de desenho habituais – régua, esquadro, transferidor, compasso, entre outros.

No que concerne à questão I, as respostas de ambas as turmas foram, praticamente, todas positivas, havendo apenas um aluno em cada turma que referiu ter gostado “mais ou menos” da aula (ver Figura 2). Na questão II, pela análise da mesma Figura, percebe-se, que os alunos da turma A estiveram mais envolvidos na tarefa do que os da turma B, no entanto, 71% destes alunos sentiram-se muito ou muitíssimo envolvidos nas tarefas enquanto na turma A, a avaliação nestes dois níveis, foi de 89%. Uma opinião semelhante ocorreu com a resposta à questão III.

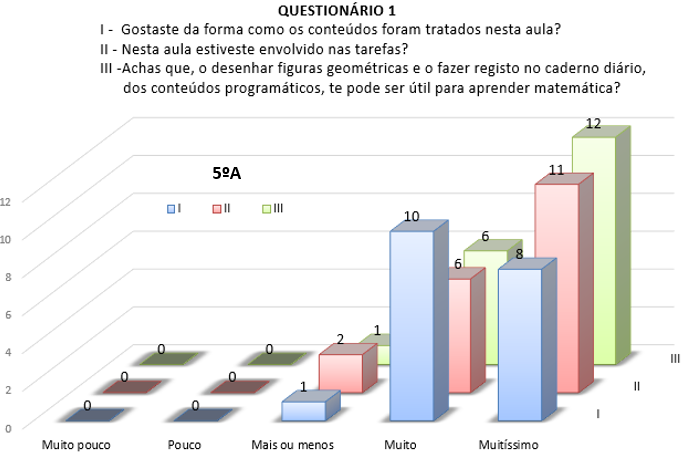
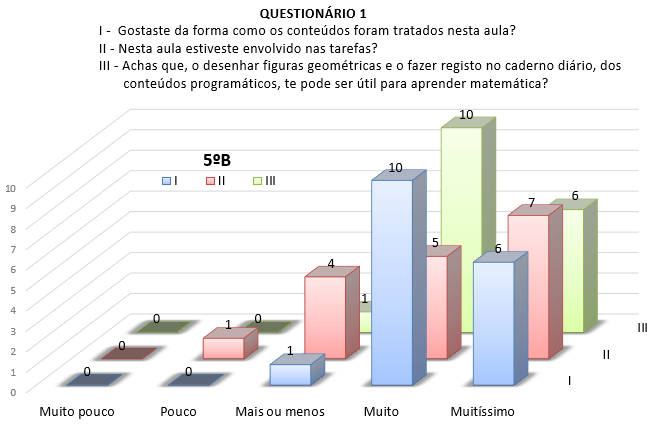
Figura 2 - Respostas às Questões referentes aos Instrumentos de Desenho como

Recurso

Na questão IV, os comentários escritos permitiram confirmar as opiniões dos alunos em relação às questões anteriores, como é possível perceber com um dos testemunhos que se apresenta na Figura 3.

Figura 3 - Opinião de um Aluno face aos Instrumentos de Desenho como Recurso

Em suma, apesar de algumas diferenças, ambas as turmas validaram e valorizaram o processo de construção do saber utilizado.

Para o ciclo de tarefas com recurso ao Geogebra, que decorreram na sala de informática, apresentaram-se guiões de exploração para que os alunos, para além de construírem lugares geométricos, verificando propriedades, realizando demonstrações e confirmando conjeturas, respondessem às questões relacionadas com as tarefas realizadas. Das observações diretas do trabalho desenvolvido pelos alunos foi possível perceber que os alunos procuravam: (1) ser criativos com os resultados finais apresentados; (2) produzir representações diferentes dos colegas; (3) partilhar as suas ideias, as suas descobertas; e (4) mostrar que tinham obtido sucesso na tarefa apresentada.

Para além destas quatro evidências no papel do aluno, foi também possível perceber que a curiosidade era um fator presente, que motivava para as propostas a realizar, implicando, também, o gosto pela aprendizagem. Os critérios de igualdade dos triângulos é um conteúdo programático que se pode afigurar de difícil compreensão por ser abstrato, quando tratado de um modo teórico. Com o Geogebra e um guião de exploração previamente construído, os alunos perceberam esses critérios e o motivo pelo qual dão origem a triângulos congruentes. Neste processo, conjeturaram e tiraram conclusões.

Analisando o questionário apresentado aos alunos, foi possível perceber um enorme envolvimento destes nesta tarefa, melhorando significativamente o ambiente de aprendizagem gerado em ambas as turmas (ver Figura 4). Não houve alunos desinteressados. Praticamente todos os alunos participaram ativamente na tarefa, embora de uma forma mais vincada no 5.º A.

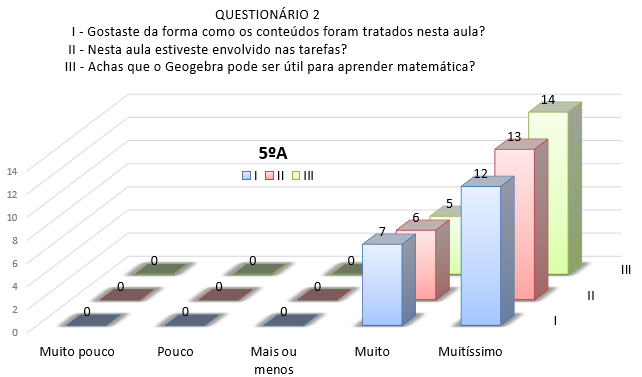
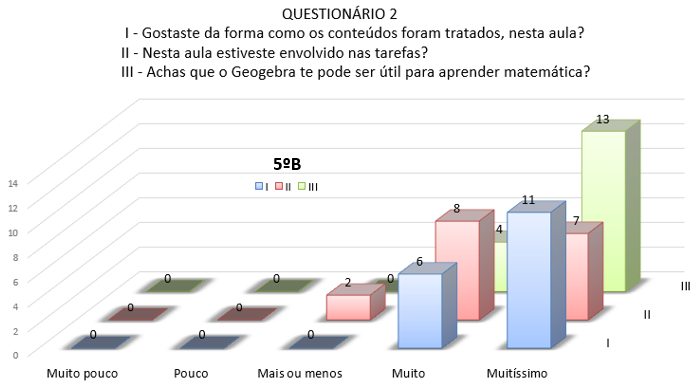
Figura 4 - Respostas às Questões I, II e III do Questionário referentes ao Geogebra

No que concerne à questão IV, na Figura 5, apresentam-se três exemplos ilustrativos do estado de espírito dos alunos sobre a utilização do Geogebra.

As plataformas do Kahoots e dos Plickers foram instrumentos chave no final do ciclo de explorações com recurso ao Geogebra, pois permitiu, a professor e alunos, uma avaliação formativa das suas aprendizagens. Estes jogos despertaram muito interesse nos alunos, tendo existido situações de euforia nas primeiras experiências. A utilização do telemóvel para responder a questões matemáticas, neste caso com o Kahoot, foi muito bem acolhida por todos. E, também neste caso, mais pelos do 5.º A do que pelos do 5.º B. Apenas dois alunos não tinham telemóvel e utilizaram o computador. Embora validassem, inequivocamente, esta ferramenta, na questão referente ao aprender, foi bastante menos entusiasta do que em relação ao Geogebra. Estas evidências podem ser observadas nos gráficos da Figura 6 que, comparado com os gráficos dos recursos anteriores, regista, na sua generalidade, um número maior de alunos posicionados no nível máximo de satisfação para com o Kahoot.

Figura 5 - Opiniões de Alunos face ao Geogebra

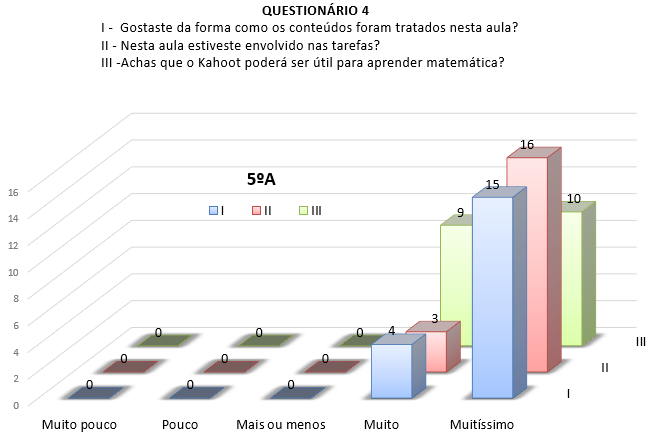
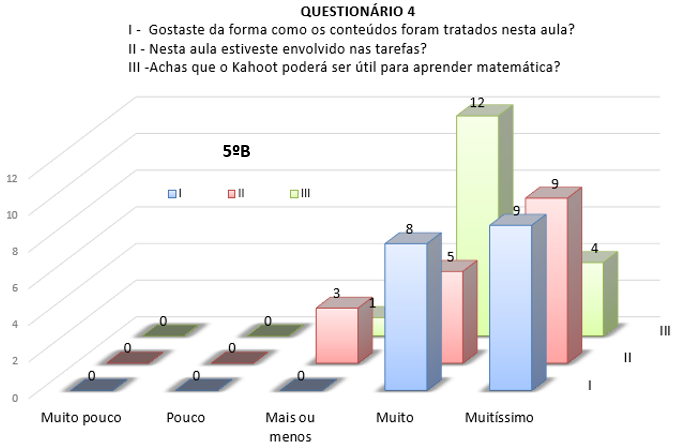
Figura 6 - Respostas às Questões I, II e III, do Questionário referente ao Kahoot

Das opiniões dos alunos apresentadas na questão IV, apesar de alguns terem escrito que aprenderam Matemática, uma parte substancial foi unânime a referir que seria uma forma de fazer revisões da matéria já abordada (ver Figura 7).

Figura 7 - Opinião de um Aluno face ao Kahoot

No que concerne ao Plickers, os alunos das duas turmas envolveram-se na proposta de trabalho e gostaram da forma como os conteúdos foram tratados. Contudo, os alunos do 5.º A não foram particularmente entusiastas com este programa, como é possível verificar com os gráficos da Figura 8 em comparação com os anteriores. Os alunos do 5.º B revelaram gostar mais do Plickers do que do Kahoot, com resultados maioritariamente no Muitíssimo (ver Figura 8). Nesta turma, mesmo ao nível do envolvimento, os resultados superaram os obtidos com o Kahoot. As turmas são diferentes e os gostos também.

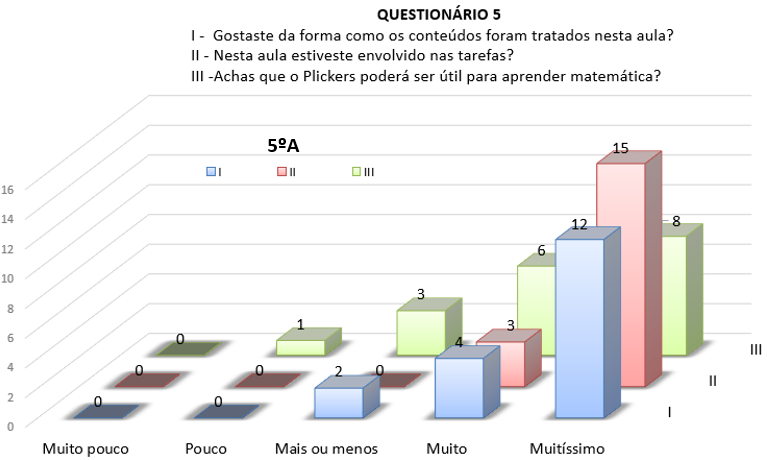
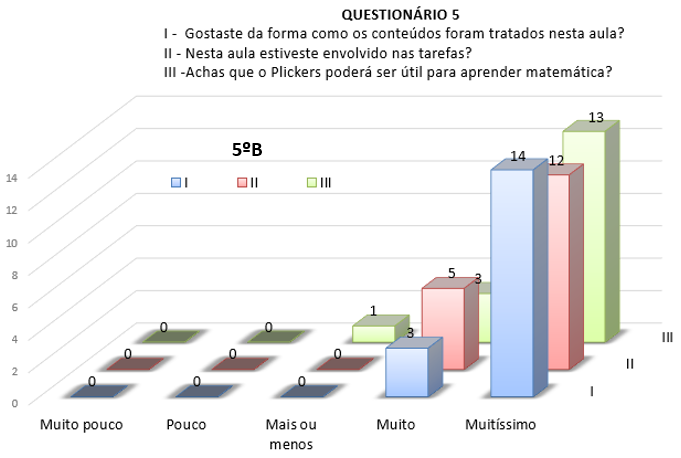
Figura 8 - Respostas às Questões I, II e III, do Questionário referente ao Plickers

Finalmente, de regresso a uma aula mais tradicional e na qual não foram utilizados quaisquer recursos, a análise das respostas ao questionário (ver Figura 9) permitiu afirmar que, um número significativo de alunos, respondeu pouco ou mais ou menos às questões colocadas. Em suma, esta foi a aula de que menos gostaram no conjunto de todas as que foram realizadas para o ensino da Geometria.

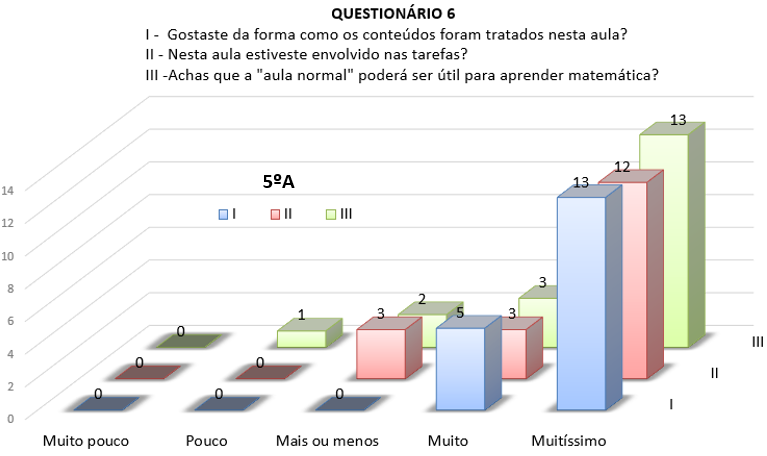
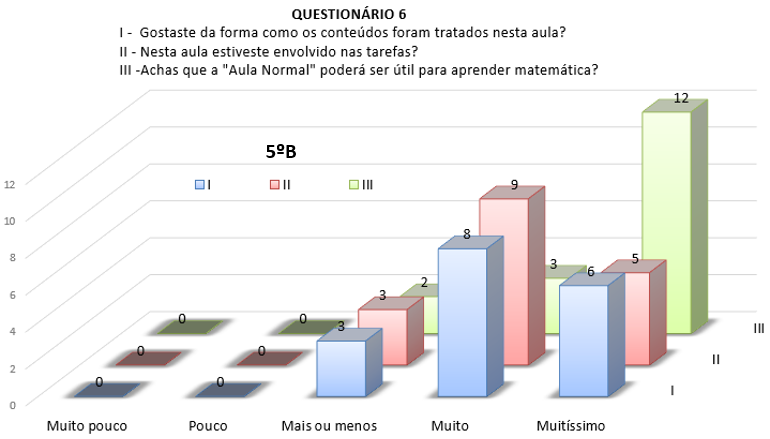
Figura 9 - Respostas às Questões I, II e III, sobre uma Aula sem Recurso à

Tecnologia

Finalmente questionou-se os alunos sobre a avaliação que atribuiriam às aulas de matemática com recurso às novas tecnologias (Geogebra, Kahoots, Plickers), tendo a esmagadora maioria atribuído nível 5. Só um número residual respondeu nível 4.

Nesta discussão sobre os resultados, apesar de a perceção dos alunos ser primordial para perceber o fator motivacional desencadeado pelas estratégias utilizadas, a avaliação formativa obtida pelas questões colocadas no Kahoot e no Plickers, são, também, uma mais-valia sobre a eficácia do processo de ensino desenvolvido. Assim, como é possível observar na Figura 10, os discentes do 5.º A tiveram um bom desempenho nos trabalhos feitos no Geogebra, com uma média de sucesso próxima dos 87%. No entanto, nas questões relacionadas com os conteúdos abordados e colocados no Plickers rondou os 76% de sucesso e no Kahoot os 61%.

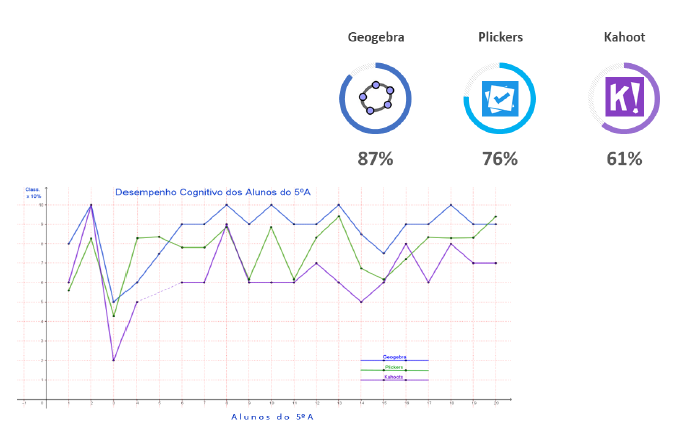
Figura 10 - Trabalhos Resolvidos com Sucesso (5.º A)

Relativamente aos alunos do 5.º B, pela análise da Figura 11, verificou-se um desempenho notável relativamente ao habitual, nos trabalhos feitos no Geogebra, com uma média próxima dos 81%. Já nas questões colocadas no Plickers acertaram com uma média de 69% e no Kahoot de 62%. Ou seja, em ambas as turmas, houve assuntos que tiveram de ser revisitados para colmatar algumas dificuldades ainda persistentes. Reter alguma informação é uma necessidade para que se processe a evolução concetual e relacional dos conteúdos abordados.

Sempre que os resultados das avaliações individuais fossem obtidas através do Kahoot ou do Plickers, ou da forma mais tradicional (teste escrito), não correspondessem aos esperados por parte do professor, os assuntos eram revisitados de forma a tentar colmatar as dificuldades ainda existentes e novo ciclo se iniciava. Este é um processo característico da metodologia de estudo ação-investigação participativa, assumida neste estudo.

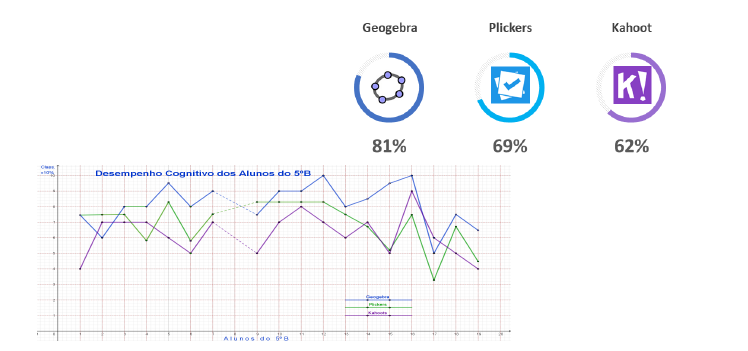
Figura 11 - Trabalhos Resolvidos com Sucesso (5.º B)

CONSIDERAÇÕES FINAIS

Na pedagogia participativa, a voz do aluno é parte integrante do seu processo de aprendizagem e, por isso, neste estudo, tornou-se indispensável ouvir as suas opiniões para o planeamento das atividades e para o professor estar sensível às suas preferências. Era indispensável, perante as situações de aprendizagem disponibilizadas, verificar não só os comportamentos de cada um face às tarefas, mas, também, o que pensam sobre estes processos de construção do saber.

A sociedade de informação coloca novas exigências à sabedoria humana e, já no presente, a escola terá de encontrar estratégias para tornar o aluno capaz de se mover à vontade no mundo da informação, usando as novas tecnologias, evidenciando os seus conhecimentos, capacidades e atitudes. De facto, tal como corroboram vários autores (e.g., Bennison & Goos, 2010; Livingstone, 2012; Maia & Couto, 2014; Olive, & Makar, 2010; Seixas et al., 2016), foi evidente que a utilização dos recursos envolvendo a tecnologia tiveram um grande impacto no interesse, na motivação e no envolvimento dos alunos nas tarefas e, consequentemente, nas suas aprendizagens. Estes foram, também, um suporte importante para o professor e alunos, fornecendo em tempo real o feedback das aprendizagens consolidadas. Os alunos tomavam consciência das suas conquistas e fragilidades, ao mesmo tempo que o professor percebia se determinado conteúdo tinha de ser, ou não, revisitado. O gosto de trabalhar com o Geogebra foi evidente quando os alunos obtiveram uma pontuação superior a 80% de sucesso nas suas descobertas, nas suas conjeturas e conclusões efetivas. A manipulação de objetos geométricos de forma livre e exploratória permitiu, a cada aluno, descobrir as relações entre objetos que o programa de Matemática contempla, mas com uma única diferença, a de que a informação não é transmitida mas é construída pelo principal agente da aprendizagem – o aluno. Esta estratégia implica que a escola leve o aluno a criar laços com o saber, fornecendo-lhe instrumentos intelectuais de emancipação, de acordo com as dificuldades manifestadas e promovendo a sociabilidade e a convivialidade. Contudo, para pensar comparativamente, é necessário reter informação, pois sem esta nada há a comparar, a relacionar e não há cognição.

No que concerne à avaliação, parte importante da função do professor (Prieto et al., 2019; Romão, 1999), é fundamental que o caminho pela avaliação formativa tenha, realmente, uma implicação nas estratégias implementadas ou no acompanhamento, mais próximo, de alguns alunos ou no retomar de um conteúdo com menor compreensão para o aluno. É neste âmbito que as plataformas do Kahoot e do Plickers foram uma mais-valia para os alunos, pois, ao mesmo tempo que os entusiasmaram e os envolveram para as abordagens na aula, num ambiente de competição saudável, recuperaram, acedendo à memória, às aprendizagens vivenciadas e construídas pelos próprios. A análise dos dados recolhidos revelou que a estratégia de gamificação teve um efeito positivo na motivação destes alunos para as tarefas, mesmo ao fim de um período de tempo mais longo como defendiam vários autores (e.g., Buckley & Doyle, 2014; Burke, 2014; Ghamdi & Holland, 2016; Sakai & Shiota, 2016). Contudo, as características específicas de cada plataforma pode ser um fator mais ou menos limitativo ou valorizado pelos alunos.

Exercitar a memória é importante, mas, nestas idades, é fundamental potenciar o desenvolvimento de outras competências como o espírito crítico, a liderança, o trabalho em grupo. Por isso, a escola deverá privilegiar o desenvolvimento cognitivo de forma a maximizar as virtualidades de qualquer uma das inteligências humanas. Aqui, não são valorizadas apenas as “formas de pensamento analítico, dedutivo, rigoroso, convergente, formal e crítico [mas também, as] formas de pensamento sintético, indutivo, expansivo, divergente, concreto e criativo, interligando-as de forma harmoniosa” (Fonseca, 2001, p. 55). Portanto, todo o processo desencadeado neste estudo teve em consideração as orientações para a prática da pedagogia diferenciada, assumindo a escola como um espaço de educação para a cidadania, uma educação para todos, que respeita os seus ritmos, os seus estilos, os tipos de inteligência, os seus contributos consideradas nas suas planificações a curto tempo. Contudo, o Estado existe para promover o bem-estar do indivíduo e, a Escola, enquanto espaço de trabalho, terá que ser, também, um espaço de vida onde os fatores motivacionais estejam presentes a fim de as funções destinadas a cada entidade sejam plenamente atingidas.

REFERÊNCIAS

Almeida, P. (1994). Imaginar para aprender: O caso da matemática. NOESIS, 32, 29-32.

Bennison, A. & Goos, M. (2010). Learning to teach mathematics with technology:

A survey of professional development needs, experiences and impacts. Mathematics Education Research Journal, 22 (1), 31-56.

Bishop, A. J., Hart, K., Lerman, S., & Nunes, T. (1993). Significant influences on children’s learning of mathematics. Paris: UNESCO.

Brearley, M. (2004). Inteligência emocional na sala de aula. São Paulo: Madras Editora Ltda.

Buckley, P. & Doyle, E. (2014). Gamification and student motivation. Interaction Learning Environment, 4820, 1–14.

Burke, B. (2014). Gamify: How gamification motivates people to do extraordinary things. Brookline: Bibliomotion, inc.

Candeias, A. A. & Almeida, L. S. (Coord.) (2007). Inteligência humana – Investigação e aplicações. Coimbra: Editora Quarteto.

Fonseca, V. (1998). Aprender a aprender – A educabilidade cognitiva. Lisboa: Editorial Notícias.

Fonseca, V. (2001). Cognição e aprendizagem. Lisboa: Âncora Editora.

Ghamdi, J. & Holland C. (2016). Exploring gamified/game-based learning in mathematics education at primary level. ECER 2016 Leading Education: The Distinct Contributions of Educational Research and Researchers, 1, 12-20.

Instituto Nacional de Estatística (2016). Inquérito à utilização de tecnologias da informação e da comunicação pelas famílias. Lisboa: INE.

Livingstone, S. (2012). Critical reflections on the benefits of ICT in education. Oxford Review of Education, 38 (1), 9-24.

Maia, C. & Couto, A. (2014). Conjeturar com o Geogebra! Sensos-e 1, 1 - 9.

Maia-Lima, C. (2016). Isometrias: As mudanças curriculares e a formação de professores. Saarbrücken: Novas Edições Académicas. ISBN:

978-3-330-75088-3

Ministério da Educação (2016). Resolução do Conselho de Ministros n.º 23/2016 - Plano Nacional de Promoção do Sucesso Escolar. Lisboa: Ministério da Educação.

Olive, J. & Makar, K. (2010). Mathematical knowledge and practices resulting from access to digital technologies. In C. Hoyles & J. Lagrange (Eds.), Mathematics education and technology – Rethinking the terrain. The 17th ICMI Study (pp. 133–177). New York: Springer.

Ponte, J. P. & Canavarro, P. (1997). Matemática e novas tecnologias. Lisboa: Universidade Aberta

Prieto, M. C., Palma, L. O., Tobías, P. B., & Léon, F. M (2019). Student assessment of the use of Kahoot in the learning process of science and mathematics.

Education Sciences, 9 (55), 2-13. doi: 10.3390/educsci9010055

Romão, J. E. (1999). Avaliação dialógica: Desafios e perspetivas. São Paulo:

Cortez Editora.

Sakai, K. & Shiota, S. (2016). A practical study of mathematics education using gamification. In P. Kommers, T. Issa, T. Issa, E. McKay & P. Isaías (Eds.), Proceedings of the International Conferences in ITS, ICEduTech and STE

(pp. 353-354). Melbourne: IADIS Press. ISBN: 978-989-8533-58-6

Seixas, L., Gomes, A. S., & De Melo Filho, I. J. (2016). Effectiveness of gamification in the engagement of students. Computers Human Behavior, 58, 48–63.

Simões, J. A., Ponte, C., Ferreira, E., Doretto, J., & Azevedo, C. (2014). Crianças e meios digitais móveis em Portugal: Resultados nacionais do projeto Net Children Go Mobile. Lisboa: Centro de